前言
PCA,即主成分分析,是一种数据降维的方法,也是一种古老而经典的人脸识别的算法。理解PCA 算法的原理和步骤,对我们的思维启发还是很有帮助的,详细的数学原理可以参考的PCA 的数学原理。虽然说在众多的人脸识别中,PCA 是较简单的,但是要想清楚了解 PCA人 脸识别的详细步骤和细节还是不容易的,尤其是对初学者而言。下面首先我详细介绍一下 PCA 人脸识别的步骤,在介绍具体实现过程。
算法步骤
-
人脸图像标准化处理 将待训练的样本图像进行标准化处理,去除背景信息,并进行人脸中心化处理,最终转化成尺寸一致的人脸图像(一般是灰度图像)。手标很麻烦,可以利用人脸检测,将人脸矩形区域提取出来。人脸检测也有相应的算法,这里不展开了。
-
构造训练样本 设一张人脸图像尺寸为$m\times{n}$,则将像素按列排开,在转置一下得到1行$mn$列的一个人脸样本,在统计学中也叫一次观测或记录,有个变量或字段,因为很大,变量的维度很高,直接处理计算复杂,且没有必要,因为这些变量肯定有相关信息。假设有$num$张人脸图像,则将所有人脸样本放在一块构成了一个样本矩阵$trainSamples$,其大小是$num\times{mn}$.
-
零均值化 求出平均脸$meanFace$,将$trainSamples$每行减去$meanFace$,得到$zeroMeantrainSamples$
-
求协方差矩阵 协方差矩阵是$num\times{num}$, 维数较高,计算量较大,采用$SVD$奇异特征值法可以减小计算量,思路是利用$zeroMeantrainSamples\cdot{zeroMeantrainSamples^{T}}$的特征向量来求上式的特征向量。
-
求协方差矩阵的特征值、特征向量 求 $cov$ 特征值 $D$、特征向量 $V_1$,并单位化正交化,得到特征向量$V$。按贡献率从高到地重新排序。取前 P 个特征值,特征向量。得到投影矩阵$T=(v_1,v_2,…v_p)$.
-
求零均值人脸样本的投影 求特征脸
-
求测试样本的零均值人脸样本并求特征脸
-
对训练样本特征脸,测试样本特征脸构造距离矩阵 对训练样本特征脸、测试样本特征脸构造距离矩阵按照最临近原则归类。
算法实现
函数设计
从整体上分为训练和测试两大函数,训练函数 pca_train 将训练的模型数据以 pca_data.mat 形式保存到当前目录。测试函数 pca_test 执行时从 pca_data.mat 从加载数据。
训练函数:
pca_train(path,trainImageNameList, newSize, trainClassType, energy)
%pca_train(path,trainImageNameList, newSize, trainClassType, energy)
%功能:根据训练样本,计算并保存classType,newSize,originSize,平均脸,特征脸,投影矩阵,到pca_data.mat
%输入:
% path:训练样本路径
% trainImageNameList:训练图像名称列表(元胞数组)
% newSize:缩减后的图像尺度
% trainClassType:训练样本类别标号(列向量)
% energy:能量比
%输出:
%保存pca_data.mat到当前目录
测试函数:
testClassType = pca_test(path, testImageNameList, trueClassType)
%testClassType = pca_test(path, testImageNameList, trueClassType)
%功能:训练样本,得到特征空间的投影矩阵,并求测试样本的类别
%输入:
% path:测试样本路径
% testImageNameList:测试图像名称列表(元胞数组)
% trueClassType:测试真实类别
%输出:
%testClassType:分类结果
数据阵准备子函数:
[samples, samplesMean, rawNum, rolNum, originSize]=arrDataMat(path, imageNameList, newSize)
%[samples, samplesMean, rawNum, rolNum, originSize]=arrDataMat(path, imageNameList, newSize)
%子函数,根据图像名称列表,读取图像数据,并灰度化,转化成 样本数*[newSize(1)*newSize(2)]数据阵
%输入:
%path:图像路径
%imageNameList:图像名称列表,类型为元胞数组
%newSize:缩减后图像尺度
%输出:
%samples:数据矩阵(一行为一个样本)
%samplesMean:数据阵平均值(行向量)
%rawNum:样本数
%rolNum:原始的变量维数,即像素的行*像素的列
%originSize:缩减前图片尺寸
特征向量施密特正交化单位化:
vv = simitzj(v, d)
%vv = simitzj(v, d)
%功能:对输入的实对称的特征值,特征向量施密特正交化,单位化
%输入:
%v:特征向量
%d:特征值
%输出:
%vv:正交化单位化后的特征向量
部分源码
function pca_train(path,trainImageNameList, newSize, trainClassType, energy)
%pca_train(path,trainImageNameList, newSize, trainClassType, energy)
%功能:根据训练样本,计算并保存classType,newSize,originSize,平均脸,特征脸,投影矩阵,到pca_data.mat
%输入:
% path:训练样本路径
% trainImageNameList:训练图像名称列表(元胞数组)
% newSize:缩减后的图像尺度
% trainClassType:训练样本类别标号(列向量)
% energy:能量比
%输出:
%保存pca_data.mat到当前目录
save('pca_data.mat','trainClassType');
fprintf('保存trainClassType到pca_data.mat成功!\n');
save('pca_data.mat','newSize','-append');
fprintf('保存newSize到pca_data.mat成功!\n');
%step1:调用子函数,计算训练样本的数据阵,和平均脸
[trainSamples, trainSamplesMean, trainNum, ~, originSize]=arrDataMat(path, trainImageNameList, newSize);
trainMeanFace = reshape(trainSamplesMean',newSize(1),newSize(2));
save('pca_data.mat','trainSamplesMean','-append');
fprintf('保存trainSamplesMean到pca_data.mat成功!\n');
save('pca_data.mat','originSize','-append');
fprintf('保存originSize到pca_data.mat成功!\n');
figure;
trainMeanFaceOriginSize = imresize(trainMeanFace, originSize);
imshow(trainMeanFaceOriginSize); %显示平均脸
title('Mean face of the training samples');
%step2:求协方差阵的特征值和向量并排序,正交化单位化,求投影矩阵
%求样本的协方差矩阵,并求特征值和特征向量,确定出降的维数,求投影矩阵
%不直接求a'a的特征值特征向量,而是采用SVD的方法,利用aa'的特征值特征向量来求a'a的特征值和向量
trainZeroMeanSamples=trainSamples-repmat(trainSamplesMean,trainNum,1);%计算零均值的人脸样本
cov = trainZeroMeanSamples*trainZeroMeanSamples';%求协方差矩阵
[v, d] = eig(cov);
lamna = diag(d);
[D, indx] = sort(lamna,1,'descend');%对特征值进行排序
rankV = v(:,indx);%对特征向量排序
t = 0;
tt = sum(D);
for i=1:trainNum %选出累积能量占%99特征值
t = t + D(i);
ratio = t/tt;
if(ratio>=energy)
break;
end
end
T_len=i;%选出特征值的个数
T2 = rankV(:,1:i);%选出特征向量
D2 = D(1:i);%选出特征值
T3 = simitzj(T2,D2); %特征向量的归一化,正交化
%求a'a的特征值特征向量,还原为原始协方差的特征向量
L = repmat((1./sqrt(D2))',trainNum,1);
T=trainZeroMeanSamples'*(T3.*L);%投影矩阵
% Data{4} = T;
save('pca_data.mat','T','-append');
fprintf('保存T到pca_data.mat成功!\n');
%step3:求训练样本的特征脸
trainNew = trainZeroMeanSamples*T; %求训练样本特征脸
% Data{5} = trainNew;
% save('Data.mat','Data');
% disp('数据保存成功!');
save('pca_data.mat','trainNew','-append');
fprintf('保存trainNew到pca_data.mat成功!\n');
end
function testClassType = pca_test(path, testImageNameList, trueClassType)
%testClassType = pca_test(path, testImageNameList, trueClassType)
%功能:训练样本,得到特征空间的投影矩阵,并求测试样本的类别
%输入:
% path:测试样本路径
% testImageNameList:测试图像名称列表(元胞数组)
% trueClassType:测试真实类别
%输出:
%testClassType:分类结果
load ('pca_data.mat','trainClassType','newSize','trainSamplesMean','T','trainNew');
%调用子函数,将测试样本转化为数据阵
[testSamples, ~, testNum]=arrDataMat(path, testImageNameList, newSize);
testZeroMeanSamples = testSamples-repmat(trainSamplesMean,testNum,1);
testNew = testZeroMeanSamples*T;%求测试样本的特征脸
n = size(trainNew,1);
m = size(testNew,1);
dis = zeros(m,n);
for i=1:m %求距离矩阵
for j=1:n
dis(i,j) = sqrt(sum((testNew(i,:)-trainNew(j,:)).^2));
end
end
K=1; %KNN最近邻的k值
[~, sortDisIndex] = sort(dis, 2, 'ascend');
KnnClassType = zeros(m, n);
for i=1:m
KnnClassType(i,:)=trainClassType(sortDisIndex(i,:))';
end
testClassType = mode(KnnClassType(:,1:K), 2);
if nargin == 3
total = length(trueClassType);
count = 0;
for i=1:total
if testClassType(i) == trueClassType(i)
count = count+1;
end
end
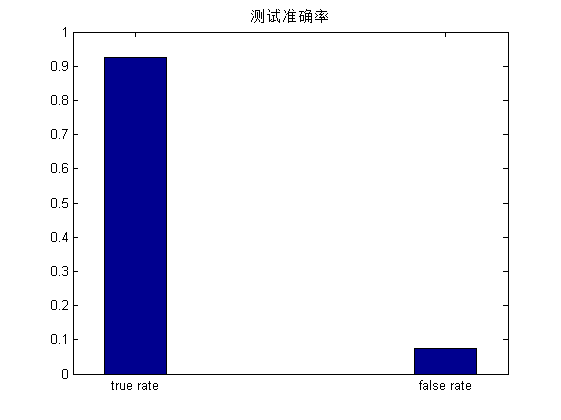
rate = count/total;
fprintf('分类的准确度是%f\n',rate);
figure;
h=bar([rate,1-rate]);
set(h,'barwidth',.2);
set(gca,'xticklabel',{'true rate','false rate'});
end
end
%子函数:准备原始数据阵
function [samples, samplesMean, rawNum, rolNum, originSize]=arrDataMat(path, imageNameList, newSize)
%[samples, samplesMean, rawNum, rolNum, originSize]=arrDataMat(path, imageNameList, newSize)
%子函数,根据图像名称列表,读取图像数据,并灰度化,转化成 样本数*[newSize(1)*newSize(2)]数据阵
%输入:
%path:图像路径
%imageNameList:图像名称列表,类型为元胞数组
%newSize:缩减后图像尺度
%输出:
%samples:数据矩阵(一行为一个样本)
%samplesMean:数据阵平均值(行向量)
%rawNum:样本数
%rolNum:原始的变量维数,即像素的行*像素的列
%originSize:缩减前图片尺寸
rawNum = size(imageNameList,1); %rawNum:样本数
rolNum=newSize(1)*newSize(2); %原始维度
samples = zeros(rawNum, rolNum);
img = imread([path,imageNameList{1}]);
originSize = size(img);
originSize = originSize(1:2);
clear img;
%准备样本矩阵
for k=1:rawNum
imageTemp_ = imread([path,imageNameList{k}]);
imageTemp = im2double(imageTemp_);
if length(size(imageTemp))==3
imageTemp = rgb2gray(imageTemp); %灰度化
imageTemp = histeq(imageTemp); %直方图均衡化
end
imageTemp2 = imresize(imageTemp, newSize);
imageTemp3 = imageTemp2(:)';
samples(k,:) = imageTemp3;
end
samplesMean = mean(samples); %样本均值
end
%子函数,进行施密特正交化,对实对称矩阵的特征向量求正交矩阵
function vv = simitzj(v, d)
%vv = simitzj(v, d)
%功能:对输入的实对称的特征值,特征向量施密特正交化,单位化
%输入:
%v:特征向量
%d:特征值
%输出:
%vv:正交化单位化后的特征向量
ii=1;
k=0;
nn=length(d);
vv=zeros(size(v));
while ii<=nn
jj=ii-k;
b=0;
while jj<ii
b=b+dot(vv(:,jj),v(:,ii))/dot(vv(:,jj),vv(:,jj))*vv(:,jj);
jj=jj+1;
end
vv(:,ii)=v(:,ii)-b;
ii=ii+1;
if ii<=nn && d(ii)==d(ii-1)
k=k+1;
else
k=0;
end
end
for ii=1:nn
vv(:,ii)=vv(:,ii)/sqrt(dot(vv(:,ii),vv(:,ii)));
end
end
function fileList=getFileList(path)
% fileList=getFileList(path)
%输入:
%path:所获取的文件列表的路径
%输出:
%fileList:path路径下文件列表,cell数组
list=dir(path);
n=size(list,1);
fileList=cell(n-2,1);
k=1;
for i=1:n
if strcmp(list(i).name,'.') || strcmp(list(i).name, '..')
continue;
end
fileList{k}=list(i).name;
k=k+1;
end
end
实验结果
平均脸:

原始人脸与重建人脸:


前特征值分布:
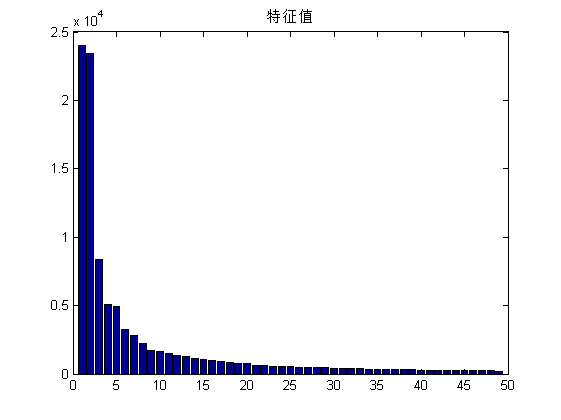
识别准确率:
前 10 个特征脸:
